Research

Conjugate heat transfer

Many real engineering applications involve non-isothermal systems where thermodynamic processes occur between solids and fluids composed of materials with distinct thermal properties, which are thermally coupled through non-adiabatic contacts. The conjugate heat transfer (CHT) problem consists in determining the temperature distribution in such multi-material domains, with specific thermodynamic laws governing heat transfer at the interfaces.

A wide range of multi-physics problems in fluid mechanics, solid mechanics, and electromagnetics involve multi-material domains and temperature-dependent phenomena, including thermomechanics, thermoelasticity, electrothermomagnetics, and fluid–thermal–structure interaction. Developing accurate and robust discretisation methods for elliptic and parabolic equations with discontinuous coefficients is therefore a critical challenge for the reliable simulation of real engineering applications.

In CHT, specific interface conditions must be prescribed depending on the nature of the contact. Typically, a discontinuous normal derivative of temperature arises from thermal energy conservation across the interface. If a perfect contact without friction is assumed, temperature remains continuous across the interface (continuity condition). In contrast, real scenarios often involve imperfect contacts with friction, which introduce an implicit temperature jump across the interface (jump condition). The accurate numerical treatment of multi-domain problems with discontinuous coefficients requires specialised interface treatments, particularly in the pursuit of high-order convergence.

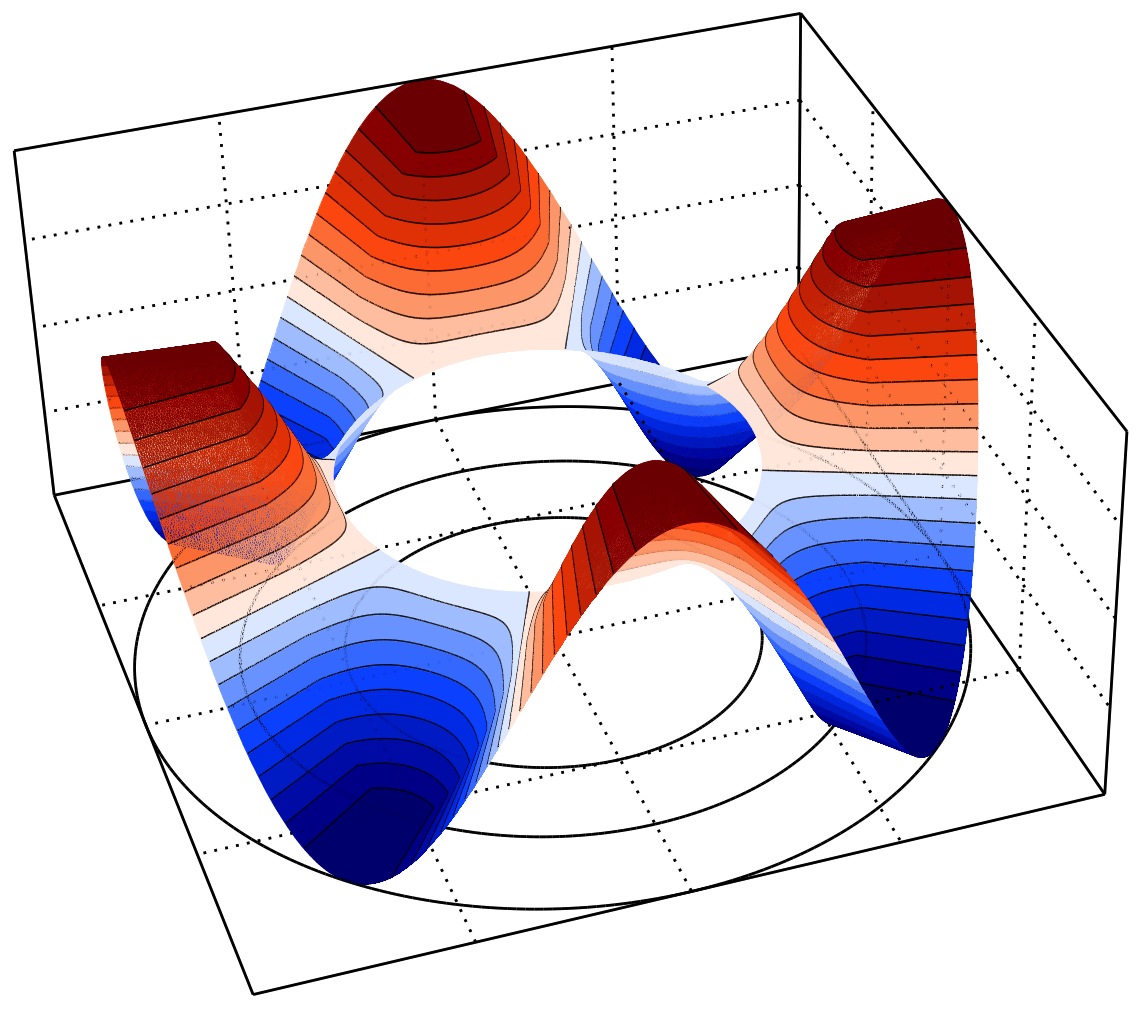
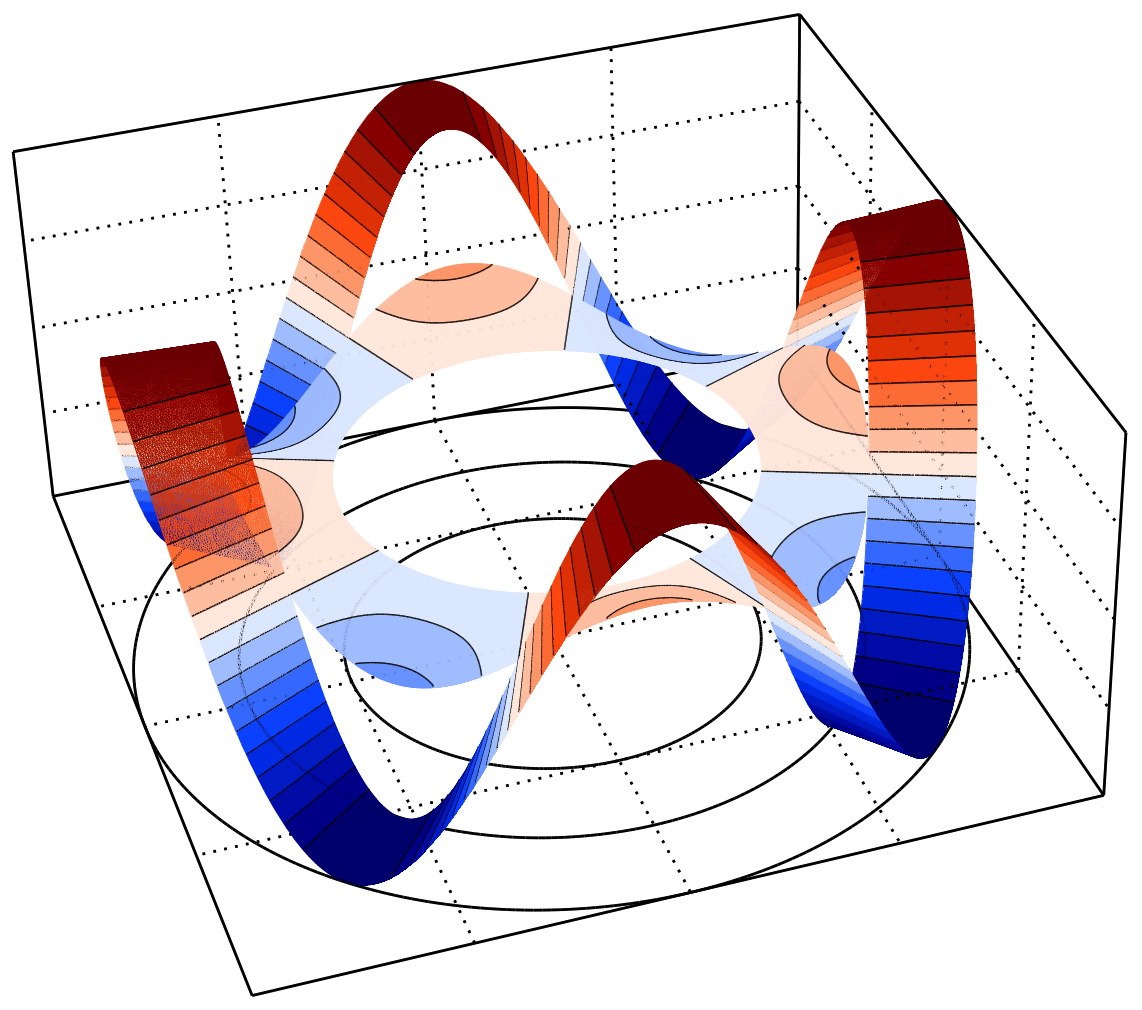
In [Costa et al., 2019; Costa et al., 2021; Costa et al., 2022], we proposed a novel technique based on Dirichlet–Neumann and Neumann–Neumann decompositions to reformulate the conjugate problem as partitioned subproblems. Each subproblem is then discretised as a conventional boundary-value convection–diffusion problem, while the thermal coupling between subdomains is enforced through constrained polynomial reconstructions at the interface. Developed in the FVM framework for 2D and 3D CHT problems with general interface conditions, the method is further enhanced with the ROD method to treat arbitrary curved interfaces, achieving up to sixth-order convergence on unstructured meshes with a piecewise linear boundary approximation.