Research
High-order accurate discretisations
Treating complex geometries is a central challenge in developing high-order accurate discretisation methods (above second order) for the numerical simulation of real engineering applications. Nevertheless, most published works address only simple domains with straight or polygonal boundaries, which substantially limits their practical applicability. In particular, the treatment of curved domains requires advanced strategies to bridge the geometrical mismatch between the physical boundary (where boundary conditions are prescribed) and the mesh boundary (where the equations are discretised).
In the finite element (FEM) paradigm, the isoparametric element method has become the standard approach to handle curved boundaries and recover optimal high-order convergence. Similar techniques have been proposed for the finite volume (FVM) and discontinuous Galerkin (DGM) methods. While effective, these approaches entail several drawbacks:
- reliance on sophisticated meshing algorithms for curved elements,
- use of cumbersome quadrature rules for integration on curved elements,
- and the need for complex nonlinear transformations between curved and standard elements.
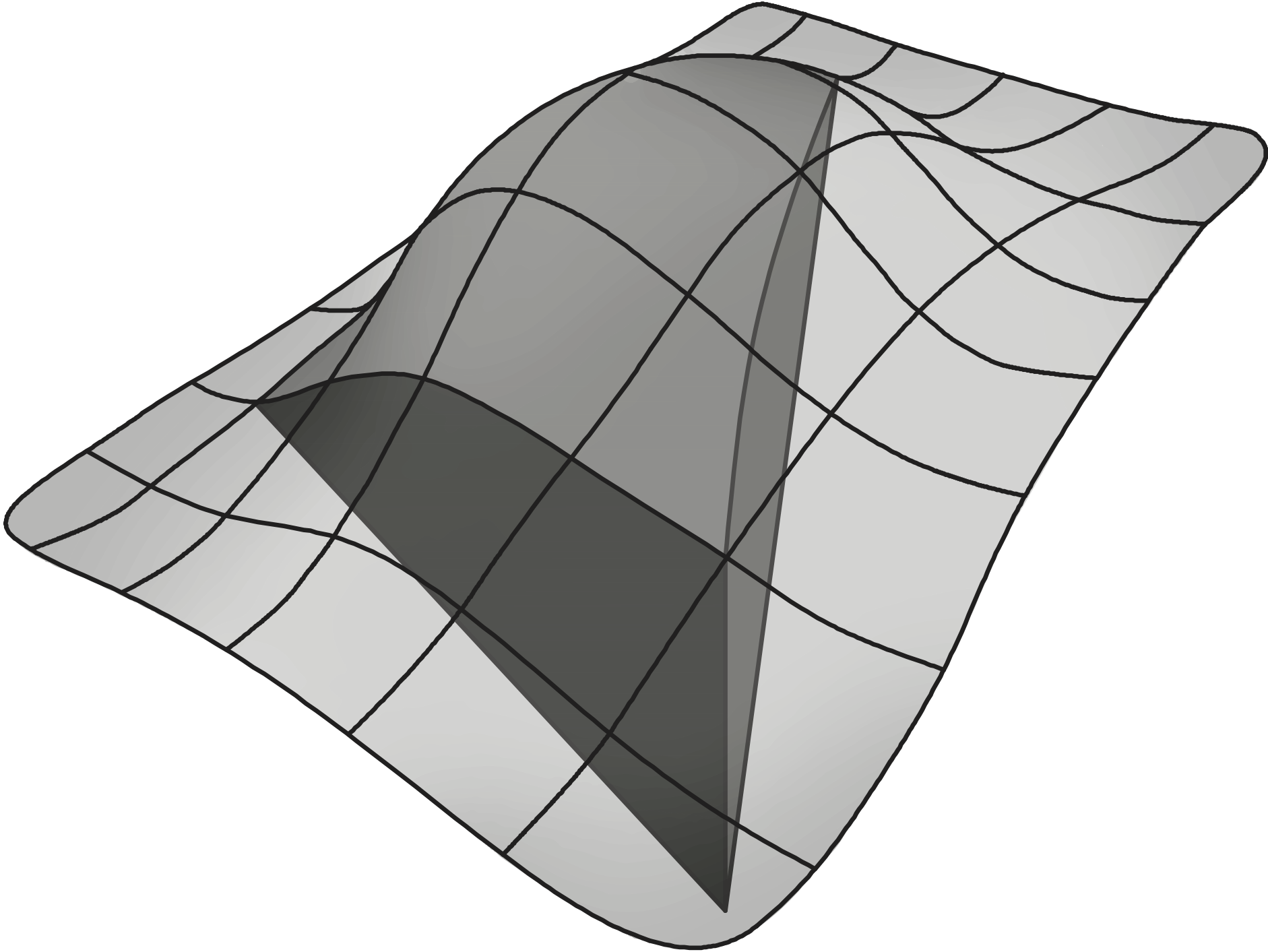
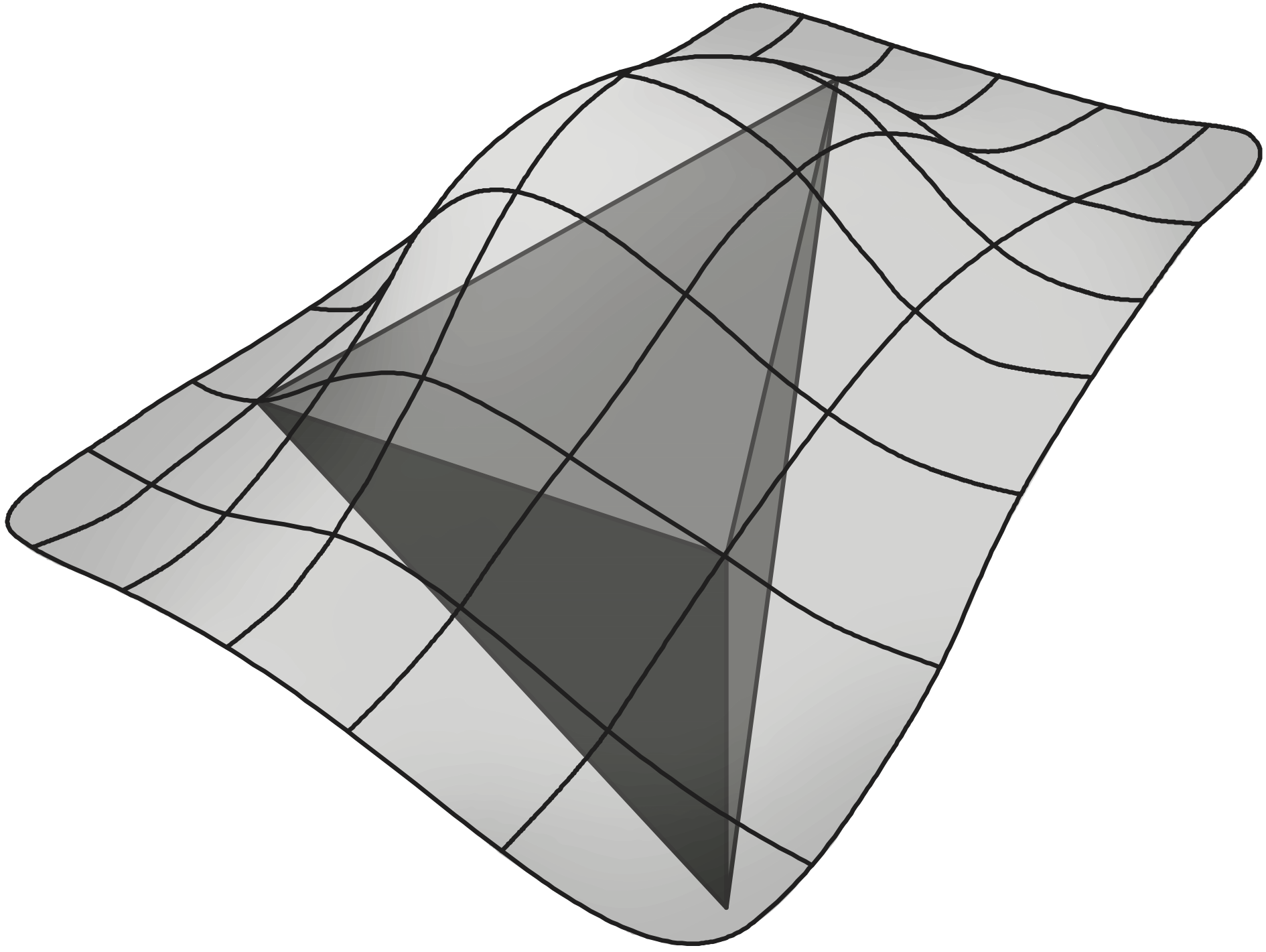
In [Costa et al., 2018; Costa et al., 2019], we introduced the reconstruction for off-site data (ROD) method, a novel strategy that achieves high-order convergence on arbitrary curved boundaries while avoiding these limitations. The ROD method transfers prescribed boundary conditions from the physical boundary to the mesh boundary using constrained polynomial reconstructions. Unknowns are defined directly on the mesh, and discretisation is performed solely on linear piecewise elements, requiring only:
- standard meshing algorithms for linear elements,
- and simple quadrature rules for integration.
Originally developed in the FVM paradigm for the 2D convection–diffusion problem with general boundary conditions, the ROD method achieves up to sixth-order convergence on unstructured meshes. The approach has since attracted considerable attention for its simplicity, efficiency, and generality in handling arbitrary boundary conditions. Extensions to the FDM and DGM frameworks have already been demonstrated successfully [Fernández-Fidalgo et al., 2020; Clain et al., 2021; Santos et al., 2024].