Research

Profile extrusion

The extrusion process plays a central role in today’s polymer processing industry, enabling the production of constant cross-section items. This continuous process relies on an extruder, where rotating screws compress and convey the raw polymeric material through the barrel. Along the barrel, multiple independently controlled heating units progressively increase the temperature to achieve melting. At the barrel outlet, an extrusion die—whose cross-section defines the geometry of the final product—forces the molten polymer under compression to flow through its openings.

Achieving a balanced flow of molten polymer at the die openings is crucial, as unbalanced flow leads to distortion of the extruded profile since thicker sections tend to draw more material than thinner ones. The conventional practice to mitigate this issue is to gradually adjust the die geometry from the barrel to the openings, compensating thinner sections with increased material flow. However, due to the complex rheological behaviour of molten polymers and the large number of process parameters involved, predicting the effect of such adjustments through analytical approaches is extremely challenging.

During the cooling stage, the cooling rate strongly influences the material structure and, consequently, the physical properties of the solidified product. High cooling rates are typically desirable—particularly for sheets and films—to suppress large crystallite formation, thus enhancing smoothness and transparency, while simultaneously increasing throughput and profitability. However, excessive cooling rates may produce solidified borders and molten cores in thicker sections, potentially causing remelting due to heat conduction. Therefore, the average temperature across the profile cross-section must fall below the polymer’s solidification point after the cooling stage. In addition, steep temperature gradients generate significant internal thermal residual stress, leading to post-processing deformations. For this reason, a uniform cooling rate across the profile is generally preferred, though this often conflicts with the desire for high cooling rates.

Addressing these challenges through traditional trial-and-error methods is resource-intensive, time-consuming, and does not guarantee optimal solutions. Consequently, computational modelling has become an indispensable tool in the polymer processing industry, effectively supporting die and process design. Nevertheless, molten polymers display complex viscoelastic behaviour governed by nonlinear constitutive equations. Accurate modelling requires the full mathematical formulation and often multiple relaxation modes, as polymer melts exhibit several characteristic timescales—each additional mode introducing six further hyperbolic equations. Numerical simulations with viscoelastic fluids therefore face stability and convergence issues, particularly when applied to industrial-scale test cases. For this reason, simplified inelastic models are frequently used in practice. While these approximations reduce computational cost and improve robustness, they cannot fully capture the physics of real viscoelastic flows, limiting predictive accuracy.

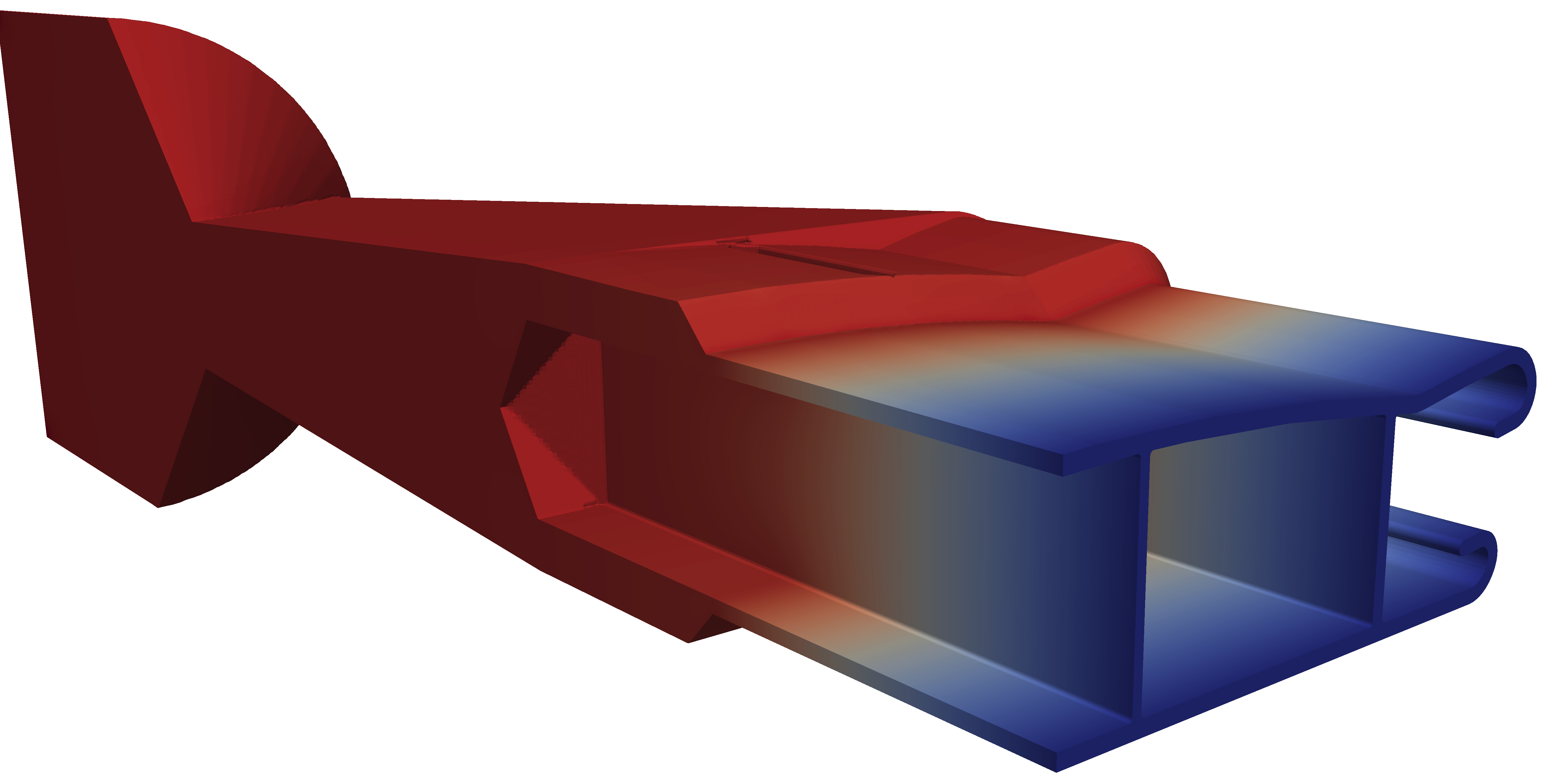
In [G.M. Magalhães et al, 2025], we developed a coupled solver for multi-mode viscoelastic flows within the foam-extend framework. In this approach, pressure, velocity, and one selected viscoelastic mode are solved simultaneously in a single block system, while the remaining modes are treated using a segregated procedure. A central question arises regarding the choice of which mode to include in the coupled system, as this decision can significantly influence both computational efficiency and solution accuracy. The study systematically analyses the effects of coupling each individual mode in a six-mode fluid for a profile extrusion case. Furthermore, a novel convergence assessment strategy is proposed, based on physically meaningful flow characteristics—such as total pressure drop and outlet flow distribution—rather than relying exclusively on numerical residuals. This physically informed metric avoids inconsistencies stemming from different residual normalisations between segregated and fully coupled solvers, providing a more robust and reliable measure of convergence across different simulation strategies.