Research

Incompressible fluid flows

The numerical solution of the Navier–Stokes equations is a cornerstone problem in computational fluid dynamics, enabling the simulation of countless engineering applications. In addition to the momentum balance equation, the system requires a mass conservation equation tailored to the flow regime. For incompressible flows, the incompressibility constraint (div–grad duality) enforces that the net mass rate of change vanishes within any control volume. Although conceptually straightforward, this constraint poses major challenges for the design of accurate, robust, and stable discretisations, particularly in the high-order context.

Several stabilisation techniques have been developed in the context of first- and second-order methods, such as staggered mesh discretisations or the classical Rhie–Chow interpolation on collocated meshes for pressure–velocity coupling. These approaches, however, do not easily extend to high-order convergence, especially on unstructured meshes.

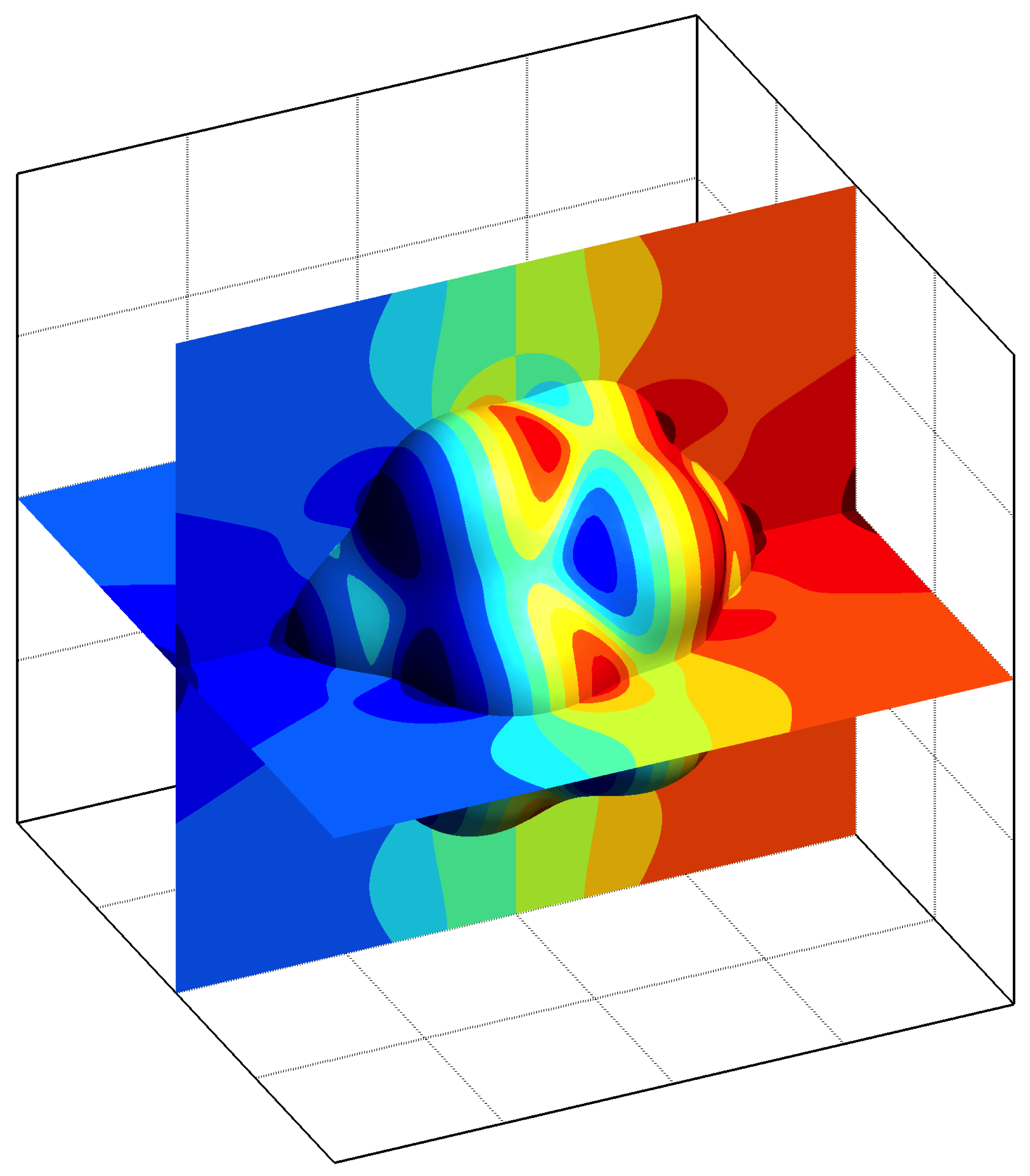
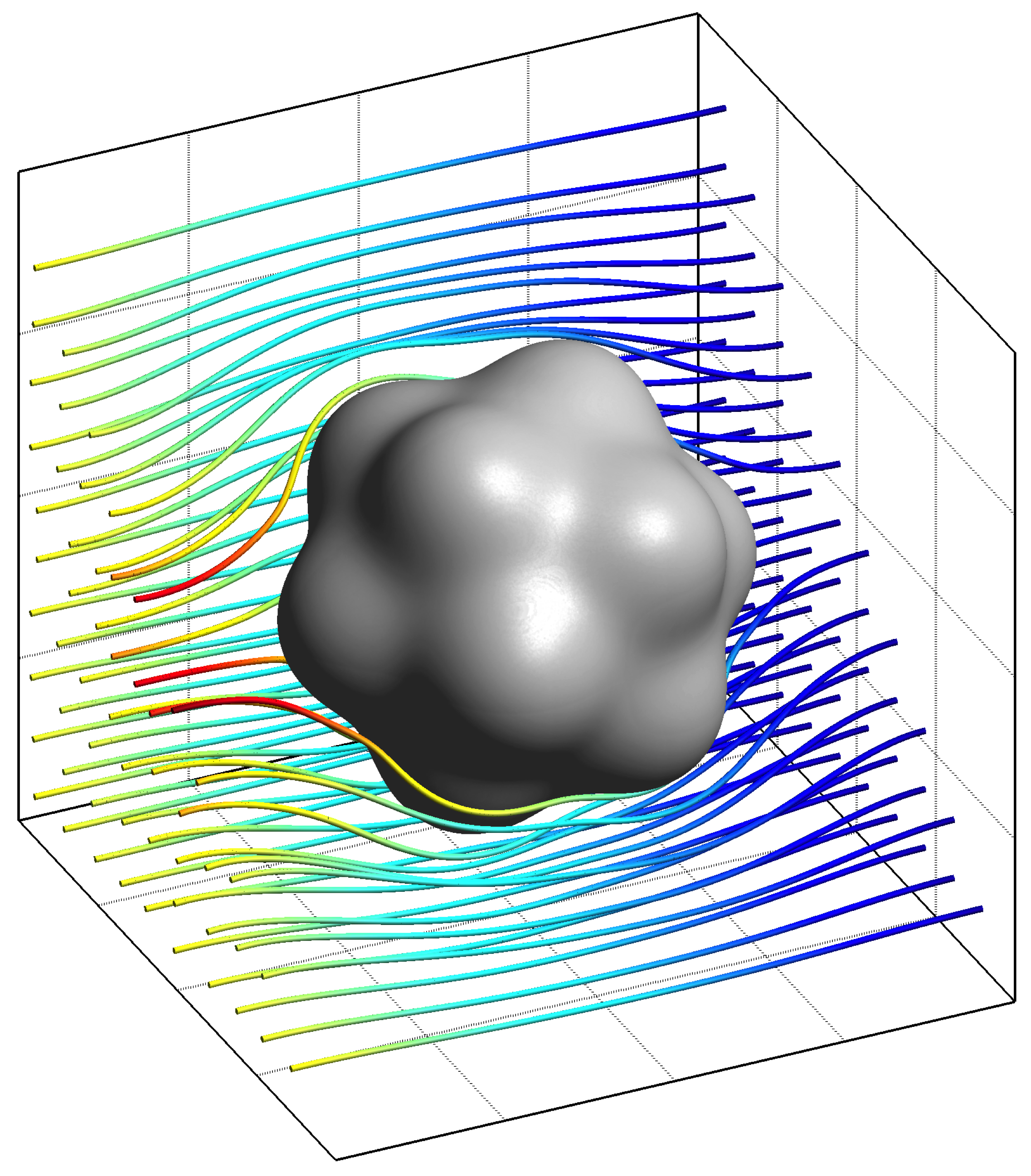
In [Costa et al., 2017; Costa et al., 2017], we proposed a very high-order accurate finite volume method (FVM) based on specialised polynomial reconstructions built on a staggered mesh framework to consistently handle the div–grad duality. The resulting velocity–pressure coupled system is further accelerated by a novel incomplete inverse preconditioning technique based on the Schur complement for saddle-point matrices. This work was later extended with the ROD method in [Costa et al., 2022; Costa et al., 2023] to address 2D and 3D incompressible flows on arbitrary curved boundaries, achieving up to sixth-order convergence on unstructured meshes with a piecewise linear boundary approximation.